
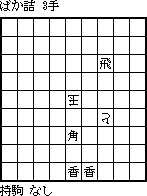
山田嘉則氏のマドラシばか詰 9手(1989年10月 将20号)の構想(復活両王手)と、その実現方法に対する花沢正純氏の建設的疑問(作意順で止めを22X打にすれば図柄が小さくなる。そうしなかった理由は何だろう?)が創作の出発点。
山田作の場合、単純に最終手を打にしようとすると角と飛の打場所が非限定になってしまう。本作では飛車・角双方をあらかじめ盤に配することでそれをうまく解消したつもり。コンパクトな初形から飛車・角の連続最遠打が飛び出す構成は気に入っている。
余談その1:持駒桂の「利き」は作意手順とは無関係であるが、桂以外だとこのルールでは完全作にはならない。
当初は左図のみ(ただし93金は歩)の単一作であった。次郎氏の「飛車と角を入れ換えたらどうなるの?」という指摘でできたのが(b)。93歩を93金にしただけで双方唯一解になったのはラッキーであった。
チェス流のツインにはなかなかなじめないが、創作の経緯はともかくとして、この結果はツインの極みと自負している。
余談その2:盤面の右辺で創作を開始した。
中出慶一氏の3手詰[1-3b]で、手数と配置のアンバランスがずっと気になっていた。あるとき(数年後だったか)ふとどこまで逆算できるか試してみた。結果、受方の飛車2枚を盤上に配置することによって舞台装置皆無の初形にまで逆算できたのは我ながらうまくいったものと思う。ただ、初出時の飛車の配置では同手数の「すかし詰」も成立したため、受方2枚の飛車の配置を絨毯爆撃で検査、「すかし詰」を認めた上で唯一解となる全11パターンを得た。途中何度も配置変更したが、玉の周りが広く空いていて飛も凝っている、つまり裸玉の香りがもっとも感じられる本図を最終図とした。
|
[1-3b] 1985年3月 フェアリーランド 中出慶一 |
|
打歩詰の定義をめぐる議論のなかで、右京氏に例題を示そうと思って創ってみたもの[1-4b]の改訂図。
詰上り図は既定の配置で、いかに攻方の使用駒(飛角角)を補充するような逆算をするのかが問題。実際には、持駒飛角角の6手で完全となる双裸玉の配置があり、またその図から持駒を1枚減らして手数を2手延ばすという逆算(+図面の平行移動)もあらゆるパターンで成功する。
つまり、持駒飛角の8手、持駒角角の8手、持駒飛の10手、持駒角の10手のそれぞれで双裸玉の完全作が得られる。
初出時はその中の持駒飛の10手版であったが、その後さらに持駒を香1枚にする4手逆算の可能性に気付き、持駒角の10手版から4手逆算したのが本図。
2手目の限定あればこそ、この逆算を採ることにした。25玉の配置で完全ならば言うことはなかったのだが。
打歩詰の定義をめぐる議論とは左図の最終手に対する58同角をどう解釈するかということ。58同角の1手があるから自殺失敗とするのか、あるいはその手では後手玉を打歩以外の手段で詰めることになるので禁手、つまり58同角とできないので自殺成立とするのか。
その後「打歩」ルールをどう解釈するかでどちらの解釈もあり得るというが結論となった。打歩詰を合法とした上で詰上りに打歩の条件付けをするものとすると自殺失敗、打歩詰を合法とした上で打歩以外の詰を禁手とすると自殺成立となる。私はむろん後者を採る。
|
[1-4b] 1997年8月 Online Fairy Mate 107号 神無太郎 |

|
加賀孝志氏の作[1-5b]の作意を一見して(出題時は解いていなかったのだ)、収束6手からの逆算がもったいないと思った。この収束はもっと自然に敷衍できるはずと感じたのである。そしてそれを最大限に実践したのが本図。
最初の試作品は角を持駒にした10手詰[1-5c]。王を囲う駒すべてを角1枚で発生させる作意は直感を100%具現化したものであった。
一度持駒にした駒を盤面に配することは手の自由後を極端に狭める気がして抵抗があるのだが、この図に関してはその代償に比してはるかに大きな果実を得ることができる。持駒の角を盤に配することによってさらに2手逆算でき、しかも余詰消しの駒をすべて消し去ることができたのだ[1-5d]。ひとつの到達点であると思う。
(どうでもいいことだが、角の配置は17の方がよかったかどうか)
さらに逆算しようとすると少し事情が変わってくる。
12手までの逆算では対駒の金銀は王手を回避する、あるいは王を包囲するという意味付けで限定できた。
しかしさらなる逆算では金銀いずれでも可という対駒を発生させる必要が出てくる。最も簡単な対処方法は金が銀のいずれか一方を売り切れ状態にすること。金だと売り切れにする駒は1枚で済むのでその方向でまとめたのが[1-5e]で、18金の配置がそれである。配置場所はどこでもよかったのだが、後続の対駒の配列に自然につながるようにしてみた。
究極の16手版は、銀を2枚配して売り切れ状態にした上で、その一方を最初に移動対させるという七郎氏のすこぶる付きのアイデアで実現された。【1-5】は七郎氏の案そのものである。
16手版はこれ以前に、一旦対駒で発生させた銀を移動対させるなどの手法で実現していたが、対駒の列に空きができるのが正に画竜点睛を欠く感じで七郎氏がこれを解消してくれたのである。
逆算中は三郎氏を始めとする神無一族の面々には多くの励ましを頂き、七郎氏の最終図につながった。一族の協力に感謝。
|
[1-5b] 1999年5月 フェアリーランド 加賀孝志 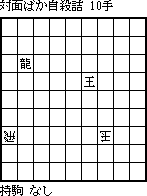
|
[1-5c] 1994年6月 Online Fairy Mate 020号 神無太郎 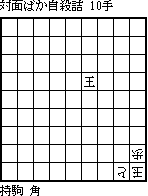
| |
|
[1-5d] 1994年3月 Online Fairy Mate 006号 神無太郎 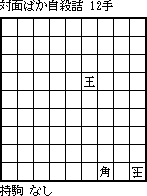
|
[1-5e] 1994年4月 Online Fairy Mate 011号 神無太郎 
|
この図の誕生の経緯はなかなか面白い。小林看空氏のフェアリーランド登場100回作戦の副産物なのである。
1999年8月の三郎邸での神無一族の会合のおり、小林看空のFL登場回数が100回に近いことが話題になり、数年来の(小林看空としての)沈黙を破って一気に登場100回のフェアリー同人をめざすことになった(と思う)。その、復帰第一作として三郎氏が作ってきたばか詰のテーマが歩の7連続合。
その作とは無関係に小林看空氏のFLへの最終登場の詰パラ1993年10月号を見ていたところ、FL結果稿の上田吉一氏のKマドラシ協力自殺詰 14手が目に止まった。そのテーマは(持駒の)歩の5連打。看空FL復帰予定作のテーマとの奇妙な暗合を感じ、歩の7連合の創作は自分には無理としても歩の連打ならなんとかなるんではと、とりあえず角の石化と復活を繰り返す歩の6連打もののKマドラシばか自殺詰をでっちあげた。
角ではこれ以上は無理そうなので、飛車に方向転換。九段目で飛車の石化と復活を繰り返す7連打もののKマドラシばか自殺の創作を初めた。これもわりあい簡単に図化することができた。初形も「ト」の字にでき、通常なら目指したものが付加価値つきで得られたということで、これで創作はお仕舞いなのだが、なんと三郎氏が歩の7連続合2回の創作への挑戦を宣言し、なおかつ実現してしまったのだ。
宣言時にはそんなものできるわけないと思っていたので驚愕と同時に7連打2回を目指さざるを得なくなった。それで、九段目の7連打の前に、1路目で歩の連打をさせる図を模索した。1路目の連打と九段目の連打はうまく連結させることができたが、1路目での7連打が達成できず、5連打がせいぜいであった。機構的に7連打は不可能で、6連打も無理な感じである。
またまた通常ならこれで創作はお仕舞いなんであるが、またまた触発媒体が出現、次郎氏試作中の逆算プログラムrfm(レトロfm:指定局面からの2手ずつの逆算とその結果表示を対話的に行うもの)である。
rfmでKマドラシばか自殺詰もサポートしたという連絡を受けて、rfmのテストのつもりで5連打+7連打の詰上りから初形への逆算手順を生成できるかを試してみた。その結果みごと逆算できた。それはそれでいいんだが、九段目から1路目への連結部分で八段目へのスムーズな連結の手も逆算してきた。八段目では7連打も可能であったため収録図が得られたという訳である。
なお、最終の自殺機構は八段目での攻防を妨げないようにするため、当初の図の機構より複雑になってしまったが、歩打での角の利きの復活と石化となり、よりテーマにふさわしいものとなったと思う。
この奇妙なルールは六郎氏の発案。マドラシや対面等のルールとの組み合わせも面白い手筋、趣向がいっぱいあるはずと六郎氏は見ている。
本図の原案も六郎氏。作意は未聞であるが、龍1枚で移動合を含め合駒を多量に発生させる狙いは本図の狙いそのもの。その原案図に早詰指摘したのが三郎氏。収束あたりで合駒ブロックを生成する手順であった。これを見逃す手はない。
まず、その合駒ブロック生成部分を純粋培養してみた。17手で飛車1回金3回を合駒で発生させる図である。この場合、角2枚金1枚銀4枚を合駒制限のみの意味付けで盤上に配する必要がある。
しばらくして23手で飛合1回金合4回の図を得た。龍の軌跡を限定するために駒2枚(例えば角2枚)を配さなければならないので、合駒制限の配置は4枚(例えば銀4枚)となる。
合駒の順序が限定できなくなるのでさらに合駒の回数を増やすことはできない。ということで、後は銀を適当な、例えば盤の端っこのほうにでも置いて一丁あがり、と済ませるつもりでいた。六郎氏もそういう表現がいいと言っていたし。
ところが悪魔がいたんですねぇ。その名は七郎。
悪魔の囁きその1:やっぱり全部の駒に合駒制限以外の意味を持たせたほうがいい。
この囁きに誘導され、玉を右上から左下に龍で追い落とすよう6手逆算して、その軌跡を銀4枚で無理矢理(非効率的にの意)限定させることに成功した。
取りあえず悪魔の条件は満たしたが、こんな逆算では、だからと言って作品の価値が上がるとも思えない。
その後、初形11龍まで逆算でき、これならば龍が 11→99 と移動するので少しストーリめいていて、まあ許せるかなと思えた。全検するには時間がかかり過ぎるので簡易検索を積み重ねていたところ、
悪魔の囁きその2:11→99 よりも 19→99のほうがいい。99→99ならもっといい。
という囁きの追い討ちがあった。それでとりあえず11→99版の完全検討を悪魔に依頼した。悪魔所有のマシンが一族内で最高のスペックだったからである。検討には数日かかると予想していたが、十数時間であっさり余詰。少なくともさらに駒を1枚置かないと余詰が解消できないことが判明した。
一旦11→99の作図は棚上げし、悪魔の囁き第二段に応えることにした。ただし、伝家の宝刀「絨毯爆撃」を以って。
つまり、盤面の右下あたりに攻方の龍と受方の玉、銀4枚を適当に配して、収束が合駒ブロックを生成する23手になるような完全作を見つけるわけである。ただしまともにfmで検討させると1題でも週のオーダの時間がかかるしろものである。知恵を絞らないと絨毯爆撃は事実上行えない。fmの各種機能を駆使して、数日で五十数万局面を試すことができた。その中から有望そうな400局くらいを候補として選定し、手で再精査し、結局、本図を4手進めたところの図を探し出すことができた。
これから2手逆算すれば初形を99龍にできるが、これも単に悪魔の囁きその2に応えただけの結果となるので、前半の手順の自然な延長となるよう4手逆算した収録図を最終図とした。
神無大九郎氏の『なりなり』シリーズ、中でも『なりなり6』に触発されて創ったもの。『なりなり6』はシリーズ中では最も手数の短かい部類だが、それでも60手である。使用駒も少なく密室型ばか自殺詰のひとつの理想の実現と言ってもいいと思う。これに触発されないようではフェアリストの名が廃ると思ったかどうか記憶は定かではないが、大九郎氏に密室型ばか自殺詰の創作方法を伝授してもうことにした。
その奥義はたった1行。愕然とした。その職人芸的な方法には唖然とするしかなかった。読者諸氏よ、奥義ゆえここに公開できないことを了とされよ。
それで『なりなり』シリーズに対抗するべく、その奥義に従って『なまなま』シリーズの創作を開始してはみたものの、なかなか長手数の完全なものはできない。番号が増えるにつれ手数も内容もだんだんと落ちて行くという情けない結果となった。ついに60手を超えられずシリーズ打ち切りを決心した頃、ひとつの素材を発見。詰上り型が1通りしかなく、しかもそれに至る手順も一通りというのものである。
この素材に対しては徹底的に「絨毯爆撃」を浴びせた。「絨毯爆撃」を繰り返すたびに手数が伸びるというなんともすばらしい素材であったからだ。
数次に渡る「絨毯爆撃」が収束しほぼ作品としての骨格を固めたとき、色気を出して2種類の序奏を付けてみた。双方とも総手数は170手。
ひとつは「絨毯爆撃」の標的にはしづらいものであったが、もう一方は完全に「絨毯爆撃」向きであったので、爆撃してみた。しかし成果はなし。つまり手で作った序奏が爆撃範囲内で最善であることを確認するに止まった。最終図は絨毯爆撃で検証済みの序奏を持つものとした。
周囲の評価は作者の思いよりはるかに高いようだ。一例に、結果稿では紙面の都合で一部のみの引用となった中村剣氏の熱い評を全文掲載しておく。
[中村剣氏解答評全文]
これはもう評価7を与えたい作品だが、評価が6までしか出来ないのが残念でならない。考えつく限りの詰形から逆算して考えると、18に攻方の銀を打たして退路封鎖しておく以外の詰形は全く無理ということが解るが、38に歩が打てないのに18に銀が打てるのだろうかと思い悩む。結局、成銀をつくるしか方法がないことに気づくが、成銀をつくる方法が39銀合からつくるより方法がないことに考えが至り、何とか解を捏ち上げるが、今度は手数がわずかにオーバーしている。攻方に歩・銀・角などの駒を渡す手順がまずいのだろうとあれこれ考え、何とか170手に収める。170手に収まってみると、あれ程起こりそうにみえた手順前後などが一切ない。この形でわずかのキズさえないなんて、そんな馬鹿なと子細に検討を重ねるが、どうしても見つからない。どうやら73手目の49銀打がすごい手で、銀を1枚多めに取っておいて、歩と交換した方が、手数が短くて済むという凄まじい理屈のせいで、一切の手順前後やキズなどが消えているようだ。まるで天使の悪戯のような、信じがたい理屈だ。この面白さが作者と解いた者にしか解らないのが無念でならない。何故皆もっと解こうとしないのだろうか。それにしても38に歩が打てない為に、歩の代わりの成銀が38に行くまでにかかる132手の何と長いことか。玉が移動するマス目はたった5マスしかないのに、まるで無辺際の宇宙を彷徨っているかのように感得せられる。本当に内容が充実し切っている。このように楽しい時間を与えてくれたことには感謝の念に堪えない。心から御礼を述べたい。私自身の人生が輝きに溢れる程、喜びに満ち満ちた数刻をありがとう。
Copyright © KAMINA Family 2001