|
■ 神無次郎氏
計算はすべて暗算で、結果をメモ用紙に書いて解きました。
で、余詰がないか、ゴミプロを作って確認しました。(^^;
だれでも確認できるように Excel VBA プログラムを添付しておきます。プロシジャ名、変数名を日本語にしてみました。再帰呼出しをしていますが、何をしているかは容易に想像できると思います。
--- ここから ---
Option Explicit
Private Const 使用中 As Boolean = True
Private Const 未使用 As Boolean = False
Private 立方数() As Long
Private 使用フラグ() As Boolean
Sub 立方数の和が2003となる数の組を求める()
Dim i As Long
i = 0
Do While i ^ 3 <= 2003
i = i + 1
ReDim Preserve 立方数(i)
ReDim Preserve 使用フラグ(i)
立方数(i) = i ^ 3
使用フラグ(i) = 未使用
Loop
Call 求解処理(0, 0)
End Sub
Private Sub 求解処理(i As Long, 合計 As Long)
Dim j As Long
Dim k As Long
j = i
Do While j ^ 3 <= 2003
j = j + 1
If 合計 + 立方数(j) >= 2003 Then '停止条件
If 合計 + 立方数(j) = 2003 Then
Dim 編集文字列 As String
For k = 1 To j - 1
If 使用フラグ(k) = 使用中 Then
編集文字列 = 編集文字列 & CStr(k) & "^3 + "
End If
Next k
MsgBox 編集文字列 & CStr(j) & "^3 = 2003"
End If
Exit Sub
End If
使用フラグ(j) = 使用中
Call 求解処理(j, 合計 + 立方数(j))
使用フラグ(j) = 未使用
Loop
End Sub
--- ここまで ---
上記マクロを Windows 98 + Excel 97 で動かすと、こんなのが表示されます。
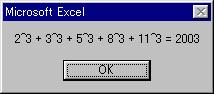
|
|
■ でこぽん氏
2003=11^3+8^3+5^3+3^3+2^3
1から12まで3乗した数を列記して
試行錯誤するという泥臭い方法で解きました。
何かエレガントな解法があるのでしょうか。
ヒントの意味もわかりませんし…
ヒントは9の剰余の求め方のつもりでした。
あまりあからさまなヒントにはならないようにしたつもりでしたが、
解法を発見してからではないと意味が判明しない類のヒントでしたか。
|
|
■ 橋本孝治氏
2003=2^3+3^3+5^3+8^3+11^3
1から12までの立方数の表を作って、大きい方から順に2003から引いて解きまし
た。ヒントは見ましたが全然活用してません。
感だけではなく腕力で解けてしまうというのは、予想外でした。
|
|
■ もず氏
懸賞2003の解答をお送りします。
11^3 + 8^3 + 5^3 + 3^3 + 2^3 = 2003
ヒントを見ずにしらみつぶしで見つけました。
このくらいだと何も考えずに計算するだけでどうにかなるようです。
ヒントは9で割った余りを考えるということですね。
立方数を9で割った余りは0,1,8のいずれかなので、
2003(余り5)を作るには最低4つの立方数が必要なことがわかります。
簡単にスクリプトを組んでみたところ、
負の立方数を許すなら4つの立方数の和でも表せるようです。
絶対値が100未満の範囲では以下のようなものがありました。
14^3 + (-13)^3 + 11^3 + 5^3 = 2003
(-70)^3 + 68^3 + 32^3 + (-13)^3 = 2003
92^3 + (-85)^3 + (-52)^3 + (-28)^3 = 2003
(-94)^3 + 83^3 + 56^3 + 44^3 = 2003
このような組み合わせはどのくらいあるのでしょうか。私にはよくわかりません。
負の立方数を許した場合、立方数の数を制限しなければ、和が2003になる組み合わせは無限にあることはすぐわかります。
立方数の数を4に限定した場合の組み合わせも無限にありそうな感じですが、よくはわかりません。
ちなみに、絶対値1000未満の範囲では51組ありました。
(-958)^3 + (-301)^3 + ( 320)^3 + ( 956)^3 = 2003
(-949)^3 + (-145)^3 + ( 617)^3 + ( 854)^3 = 2003
(-913)^3 + (-271)^3 + ( 395)^3 + ( 896)^3 = 2003
(-829)^3 + (-727)^3 + ( 416)^3 + ( 959)^3 = 2003
(-829)^3 + (-481)^3 + ( 161)^3 + ( 878)^3 = 2003
(-775)^3 + ( 212)^3 + ( 545)^3 + ( 665)^3 = 2003
(-766)^3 + ( 299)^3 + ( 464)^3 + ( 686)^3 = 2003
(-763)^3 + ( 158)^3 + ( 311)^3 + ( 743)^3 = 2003
(-751)^3 + (-322)^3 + ( 179)^3 + ( 767)^3 = 2003
(-727)^3 + (-103)^3 + ( -79)^3 + ( 728)^3 = 2003
(-685)^3 + (-178)^3 + ( 434)^3 + ( 626)^3 = 2003
(-661)^3 + (-460)^3 + ( 68)^3 + ( 728)^3 = 2003
(-661)^3 + (-388)^3 + ( 290)^3 + ( 686)^3 = 2003
(-607)^3 + (-157)^3 + ( 392)^3 + ( 551)^3 = 2003
(-604)^3 + (-160)^3 + (-154)^3 + ( 611)^3 = 2003
(-559)^3 + (-109)^3 + ( 71)^3 + ( 560)^3 = 2003
(-556)^3 + ( 323)^3 + ( 353)^3 + ( 455)^3 = 2003
(-550)^3 + (-154)^3 + ( -13)^3 + ( 554)^3 = 2003
(-514)^3 + ( 155)^3 + ( 395)^3 + ( 413)^3 = 2003
(-514)^3 + ( 182)^3 + ( 323)^3 + ( 458)^3 = 2003
(-511)^3 + (-400)^3 + (-313)^3 + ( 611)^3 = 2003
(-511)^3 + (-262)^3 + ( 5)^3 + ( 533)^3 = 2003
(-490)^3 + (-328)^3 + (-154)^3 + ( 539)^3 = 2003
(-469)^3 + (-244)^3 + (-142)^3 + ( 494)^3 = 2003
(-469)^3 + (-202)^3 + ( 353)^3 + ( 407)^3 = 2003
(-460)^3 + ( 17)^3 + ( 359)^3 + ( 371)^3 = 2003
(-454)^3 + (-133)^3 + ( -52)^3 + ( 458)^3 = 2003
(-436)^3 + (-409)^3 + ( -49)^3 + ( 533)^3 = 2003
(-418)^3 + ( 140)^3 + ( 323)^3 + ( 332)^3 = 2003
(-415)^3 + ( -91)^3 + ( 149)^3 + ( 410)^3 = 2003
(-355)^3 + ( 125)^3 + ( 161)^3 + ( 338)^3 = 2003
(-346)^3 + (-157)^3 + ( 56)^3 + ( 356)^3 = 2003
(-328)^3 + (-112)^3 + ( 179)^3 + ( 314)^3 = 2003
(-328)^3 + ( 35)^3 + ( 182)^3 + ( 308)^3 = 2003
(-325)^3 + ( 116)^3 + ( 209)^3 + ( 287)^3 = 2003
(-322)^3 + ( -10)^3 + ( 251)^3 + ( 260)^3 = 2003
(-292)^3 + (-226)^3 + ( 140)^3 + ( 323)^3 = 2003
(-289)^3 + ( -94)^3 + ( 161)^3 + ( 275)^3 = 2003
(-283)^3 + ( 140)^3 + ( 209)^3 + ( 221)^3 = 2003
(-271)^3 + ( 119)^3 + ( 134)^3 + ( 251)^3 = 2003
(-220)^3 + (-163)^3 + ( 65)^3 + ( 245)^3 = 2003
(-217)^3 + ( -73)^3 + ( 149)^3 + ( 194)^3 = 2003
(-202)^3 + (-196)^3 + ( -34)^3 + ( 251)^3 = 2003
(-181)^3 + ( -46)^3 + ( 8)^3 + ( 182)^3 = 2003
(-133)^3 + ( -73)^3 + ( -7)^3 + ( 140)^3 = 2003
(-130)^3 + ( 32)^3 + ( 98)^3 + ( 107)^3 = 2003
(-103)^3 + ( -31)^3 + ( -7)^3 + ( 104)^3 = 2003
( -94)^3 + ( 44)^3 + ( 56)^3 + ( 83)^3 = 2003
( -85)^3 + ( -52)^3 + ( -28)^3 + ( 92)^3 = 2003
( -70)^3 + ( -13)^3 + ( 32)^3 + ( 68)^3 = 2003
( -13)^3 + ( 5)^3 + ( 11)^3 + ( 14)^3 = 2003
|
|
■ 若林広氏
若林です。2年ぶりに年賀出題に解答します。
<解答>
2*2*2 + 3*3*3 + 5*5*5 + 8*8*8 + 11*11*11 = 2003
<経緯>
とりあえず1〜12の立法数とにらめっこして一つの解を発見。
あらためてヒントの意味を考える。
・3,9で割ったときのあまりを考えると絞り込みやすい。
・左辺に意味はなく、5つの数字の和である。
いずれも決め手に欠ける。ヒントの意味が理解できず、美しく解けずに残念。
その後一応全検しました。
#!/usr/bin/perl
for ($a = 0 ; $a <= 1; $a++) {
for ($b = 0 ; $b <= 1; $b++) {
for ($c = 0 ; $c <= 1; $c++) {
for ($d = 0 ; $d <= 1; $d++) {
for ($e = 0 ; $e <= 1; $e++) {
for ($f = 0 ; $f <= 1; $f++) {
for ($g = 0 ; $g <= 1; $g++) {
for ($h = 0 ; $h <= 1; $h++) {
for ($i = 0 ; $i <= 1; $i++) {
for ($j = 0 ; $j <= 1; $j++) {
for ($k = 0 ; $k <= 1; $k++) {
for ($l = 0 ; $l <= 1; $l++) {
if ($a*1 + $b*8 + $c*27 + $d*64 + $e*125 + $f*216 + $g*343 ←改行入れました
+ $h*512 + $i*729 + $j*1000 + $k*1331 + $l*1728 == 2003) {
print "$a,$b,$c,$d,$e,$f,$g,$h,$i,$j,$k,$l\n";
}
}}}}}}}}}}}
こちらのスクリプトの方がわかりやすいですね。
(すみません、表示上の都合でスクリプトの一部を勝手に改行してます)
・3,9で割ったときのあまりを考えると絞り込みやすい。
という解釈はヒントの意図どおりでしたが、決めて手に欠けましたか...
|
|
