|
| 仭丂栤戣 |
丒 |
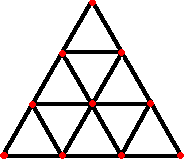
侾曈偺挿偝偑侾偺挻棫曽懱撪偵侾俈屄偺揰傪偲傝傑偡丅
偙偺偲偒丄嵟傕嬤偄俀揰娫偺嫍棧偺嵟戝抣偼丠 |
|
丒 |
挻棫曽懱偲偼係師尦偺棫曽懱偺偙偲偱偡丅偙傫側姶偠偱偡丅柍悎偱偡傒傑偣傫丅
俠亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝侾丆侽亝倄亝侾丆侽亝倅亝侾丆侽亝倂亝侾乸 |
|
| 仭丂夝摎 |
丒 |
嵟傕嬤偄俀揰娫偺嫍棧偺嵟戝抣偼侾丅 |
|
丒 |
夝摎幰偼丄庒椦峀巵丄傕偢巵丄愒栘梍岾巵丄恄柍幍榊巵丄娭彑庻巵丄晲揷棽巌巵丄愳暲梞懢丄暯愇巌偺俉柤乮夝摎摓拝弴乯丅徹柧偺桳柍丄尩枾惈偼偲傕偐偔丄慡堳惓夝偱偟偨丅 |
|
丒 |
尩惓側傞拪慖偺寢壥丄寽徿摉慖幰偼埲壓偺偲偍傝偲側傝傑偟偨丅
乽曄尪帺嵼乿丗娭彑庻巵
乽儁儞僔儖丒僷僘儖乿丗晲揷棽巌巵
|
|
| 仭丂夝愢 |
丒 |
俠傪侾曈偺挿偝偑侾乛俀偺彫挻棫曽懱偵侾俇暘妱偟傑偡丅彮側偔偲傕侾偮偺彫挻棫曽懱偵偼侾俈屄偺揰偺偆偪俀屄偑娷傑傟偰偄傞偼偢偱偡丅
偦偺俀揰娫偺嫍棧偺嵟戝抣偼乮乮侾乛俀乯丱俀亄乮侾乛俀乯丱俀亄乮侾乛俀乯丱俀亄乮侾乛俀乯丱俀乯丱乮侾乛俀乯亖侾丅
偮傑傝丄偳偆婃挘偭偰傕俀揰娫偺嫍棧偺嵟彫抣偺嵟戝抣偼侾傪挻偊傑偣傫丅
堦曽偱丄侾俈屄偺揰傪師偺傛偆偵偲傞偲丄偳偺俀揰娫偺嫍棧傕侾埲忋偵側偭偰丄侾偑摎偩偲傢偐傝傑偡丅
乮侽丆侽丆侽丆侽乯丄乮侽丆侽丆侽丆侾乯丄乮侽丆侽丆侾丆侽乯丄乮侽丆侽丆侾丆侾乯丄
乮侽丆侾丆侽丆侽乯丄乮侽丆侾丆侽丆侾乯丄乮侽丆侾丆侾丆侽乯丄乮侽丆侾丆侾丆侾乯丄
乮侾丆侽丆侽丆侽乯丄乮侾丆侽丆侽丆侾乯丄乮侾丆侽丆侾丆侽乯丄乮侾丆侽丆侾丆侾乯丄
乮侾丆侾丆侽丆侽乯丄乮侾丆侾丆侽丆侾乯丄乮侾丆侾丆侾丆侽乯丄乮侾丆侾丆侾丆侾乯丄
乮侾乛俀丆侾乛俀丆侾乛俀丆侾乛俀乯 |
|
丒 |
侾俇暘妱偟偨彫挻棫曽懱偼偙傫側姶偠偵側傝傑偡丅柍悎偱偡傒傑偣傫丅
俠侾亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆侽亝倅亝倛丆侽亝倂亝倛乸
俠俀亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆侽亝倅亝倛丆倛亝倂亝侾乸
俠俁亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆倛亝倅亝侾丆侽亝倂亝倛乸
俠係亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆倛亝倅亝侾丆倛亝倂亝侾乸
俠俆亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亝倄亝侾丆侽亝倅亝倛丆侽亝倂亝倛乸
俠俇亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亝倄亝侾丆侽亝倅亝倛丆倛亝倂亝侾乸
俠俈亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亝倄亝侾丆倛亝倅亝侾丆侽亝倂亝倛乸
俠俉亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亝倄亝侾丆倛亝倅亝侾丆倛亝倂亝侾乸
俠俋亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆侽亝倄亝倛丆侽亝倅亝倛丆侽亝倂亝倛乸
俠侾侽亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆侽亝倄亝倛丆侽亝倅亝倛丆倛亝倂亝侾乸
俠侾侾亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆侽亝倄亝倛丆倛亝倅亝侾丆侽亝倂亝倛乸
俠侾俀亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆侽亝倄亝倛丆倛亝倅亝侾丆倛亝倂亝侾乸
俠侾俁亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆倛亝倄亝侾丆侽亝倅亝倛丆侽亝倂亝倛乸
俠侾係亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆倛亝倄亝侾丆侽亝倅亝倛丆倛亝倂亝侾乸
俠侾俆亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆倛亝倄亝侾丆倛亝倅亝侾丆侽亝倂亝倛乸
俠侾俇亖乷乮倃丆倄丆倅丆倂乯乥倛亝倃亝侾丆倛亝倄亝侾丆倛亝倅亝侾丆倛亝倂亝侾乸
偨偩偟丄倛亖侾乛俀偱偡丅 |
|
仭丂庒椦峀巵
<夝摎>
挻棫曽懱傪堦曈1/2偺挻棫曽懱16屄偵暘妱偡傞丅
昁偢偳偙偐偺挻棫曽懱偵俀偮偺揰偑懚嵼偡傞偺偱丄
嵟戝抣偺忋尷偼懳妏慄忋偵俀揰偑偁傞応崌偱丄
sqrt((1/2)^2 * 4) = 1丅
幚椺偑懚嵼偡傞偙偲偼偼帵偡傑偱傕側偄偺偱徣棯丅
<姶憐>
偆乕傫乧乧挻棫曽懱偱偺數偺憙尨棟偱偡偐丅
偪傚偭偲抦偭偰偄傞恖偵偼弖娫偱丄抦傜側偄恖偵偼
尒岦偒傕偝傟側偄丄尩偟偄栤戣偵側偭偰偟傑偭偨傛偆側丅
摎偊偑惍悢側偺偑桞堦偺尒強偱偟傚偆偐丅
慜夞偵偣傑傞夝摎幰悢偑偁偭偰丄偪傚偭偲價僢僋儕偟偰偄傑偡丅
摎偼侾寧偵偪側傫偱偲偄偆偙偲偱丅
|
|
仭丂傕偢巵
挻棫曽懱偺捀揰16屄偲偦偺拞怱1屄偵攝抲偟偨偲偒偺挿偝偑亂1亃偵側傝傑偡丅
偙傟偑嵟戝抣丅
挻棫曽懱傪x,y,z,w=1/2偺柺偱愗傞偲丄1曈偺挿偝偑1/2偺挻棫曽懱偑16屄偱偒傑偡丅
揰偼17屄偁傞偺偱丄16屄偺挻棫曽懱偺偆偪彮側偔偲傕1偮偼丄2偮埲忋偺揰傪娷傒傑偡丅
偦偺2偮偺揰傪偱偒傞偩偗棧偟偰攝抲偡傞偵偼
懳妏慄偱岦偐偄崌偆2偮捀揰偵抲偔偟偐偁傝傑偣傫丅
1曈偺挿偝偑1/2偺挻棫曽懱偺懳妏慄偺挿偝偼丄
{ (1/2)^2 + (1/2)^2 + (1/2)^2 + (1/2)^2 }^(1/2) = 1
側偺偱丄偙傟偑摎偊偱偡丅
乽數偺憙乿傪巊傢側偄夝朄偼側偄傫偱偡偐偹偉丅
|
|
仭丂愒栘梍岾巵
夝摎丗1
夝朄丗
堦曈偑1偺挻棫曽懱偵17屄偺揰傪庢傞偲
堦曈偑1/2偺挻棫曽懱偵16摍暘偟偨応崌丄彮側偔偲傕1偮偺挻棫曽懱偵2屄埲忋偺
揰偑庢傜傟傞偙偲偵側傞丅
嵟傕嬤偄俀揰娫偺嫍棧偺嵟戝抣偲側傞偺偼丄師偺傛偆偵揰偑庢傜傟偨応崌偱偁傞
丒堦曈偑1/2偺挻棫曽懱偺16屄偺偆偪15屄偵偼1屄偩偗揰偑庢傜傟傞
丒巆傝偺挻棫曽懱偵2屄偺揰偑庢傜傟傞
丒偙偺2屄偺揰偑挻棫曽懱偺捀揰偵偁傞
傛偭偰
(1/2)^2+(1/2)^2+(1/2)^2+(1/2)^2=1
(1)^(1/2)=1
亪1
丂
姶憐
乽壗偲偐偺憙偺尨棟乿偲屇偽傟偰偄偨傛偆側婥偑偟傑偡丅
(偙傟偑惓幃側屇傃曽偐偳偆偐偼晄柧偱偡)
丂
夝朄偼偁偭偰偄傞偲巚偄傑偡偑寁嶼偑偙傟偱傛偄偺偐帺怣偑偁傝傑偣傫丅
丂
帡偨傛偆側栤戣偱70亊70偺惓曽宍偱50屄偺揰傪偲傞偲偄偆栤戣偑偁傝傑偟偨丅
偙偺栤戣偩偲丄嵟戝抣傪媮傔傞偺偼擄偟偦偆偱偡偹丅
惓曽宍傪係俋暘妱偟偰乽數偺憙尨棟乿傪揔梡偟偰傕丄侾侽亊侾侽偺惓曽宍偱俀揰傪娷傓傕偺偑懚嵼偡傞丄偲偄偆偙偲偟偐帵偣傑偣傫偐傜丄
嵟戝抣偼10併俀乮佮侾係丏侾係俀丒丒丒乯埲壓偲偄偆峳偄昡壙偟偐偱偒側偄偱偡偹丅乮傕偭偲偆傑偄暘妱偑偁傞偐偟傜傫乯
壓婰偺傛偆側攝抲乮俆俀屄偱偡偑乯偑偁傞偺偱丄嵟戝抣偼俆乮併侾俋俁乯乛俇乮佮侾侾丏俆俈俈丒丒丒乯埲忋偵偼側傞傛偆偱偡丅乮侾侽併俀偲偼偩偄傇嵎偑偁傞乯
丂
丂
惓嶰妏宍偺撪晹偵侾侽屄偺揰傪偲傞丄偲偄偆傾儗儞僕偼偳偆偱偟傚偆偐丅
擭夑嶼偵偼側偭偰偄傑偣傫偑丄寢峔僗儅乕僩偐偲丅
丂
|
|
仭丂恄柍幍榊巵
摎偊丗侾
丂
16屄偺揰傪挻棫曽懱偺奺捀揰偵抲偒丄傕偆侾屄偺揰傪恀傫拞(0.5,0.5,0.5,0.5)
偵抲偄偨偲偒偵偙偺抣偵側傝傑偡丅
徹柧偼儃儘偑弌傞偲偄偗側偄偺偱徣棯偟傑偡乮懧棊乯丅
徹柧傑偱偼媮傔偰偄傑偣傫偺偱偛埨怱傪丅
|
|
仭丂娭彑庻巵
夝摎
丂侾俇揰傪挻棫曽懱偺捀揰偵丄侾揰傪廳怱 (1/2,1/2,1/2,1/2) 偵攝抲偡傞丅
丂偙偺偲偒偺捀揰偲廳怱偲偺嫍棧偼侾偲側傞丅偙傟偑媮傔傞抣偱偁傞丅
丂
徹柧
丂尩枾側徹柧偼擄偟偦偆偱偡偹丅偱偡偑丄姶妎揑偵傎傏娫堘偄側偄偱偟傚偆丅
攝抲偑偙傟埲奜偵側偄偙偲偺僄儗僈儞僩側徹柧偼傑偩尒偮偗偰偄傑偣傫丅
丂
晽傒偳傝偝傫偲偺傗傝偲傝傪儊儌偟偰偍偒傑偡丅
丂
晽傒偳傝偺嬍庤敔丂2005擭01寧01擔
晽傒偳傝偺嬍庤敔丂2005擭01寧26擔
Seki's Diary丂2005擭01寧26擔
丂
搒拀戩巌挊偺乽巐師尦偺悽奅乿乮僽儖乕僶僢僋僗乯偼偍慐傔偱偡丅挻棫曽懱偑僀儊乕僕偱偒傞傛偆偵側偭偰偟傑偆偐傕偟傟傑偣傫丅
|
2005擭2寧9擔捛婰
丂
暯愇偝傫偐傜丄攝抲偑偙傟埲奜偵側偄偙偲偺徹柧傪偄偨偩偒傑偟偨丅
惛嵏偟偨偁偲宖嵹偟傛偆偲巚偭偰偄傑偟偨偑丄偦偺尦婥偑側偄偺偲丄偨傇傫戝忎晇偦偆側偺偲丄
儊乕儖傪偄偨偩偄偰偐傜俀擔宱偭偰偟傑偭偨偺偱丄嵹偣偰偟傑偄傑偡丅
丂
丂傑偢丄侾俇屄偺挻棫曽懱偺僽儘僢僋偵暘妱偟傑偡丅偨偩偟丄嫬奅慄偺婣懏傪偼偭偒
傝偝偣傑偡丅嬶懱揑偵偼偨偲偊偽丄
俠01亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆侽亝倅亝倛丆侽亝倂亝倛乸
俠02亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆侽亝倅亝倛丆倛亙倂亝侾乸
俠03亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆倛亙倅亝侾丆侽亝倂亝倛乸
俠04亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆侽亝倄亝倛丆倛亙倅亝侾丆倛亙倂亝侾乸
俠05亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亙倄亝侾丆侽亝倅亝倛丆侽亝倂亝倛乸
俠06亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亙倄亝侾丆侽亝倅亝倛丆倛亙倂亝侾乸
俠07亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亙倄亝侾丆倛亙倅亝侾丆侽亝倂亝倛乸
俠08亖乷乮倃丆倄丆倅丆倂乯乥侽亝倃亝倛丆倛亙倄亝侾丆倛亙倅亝侾丆倛亙倂亝侾乸
俠09亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆侽亝倄亝倛丆侽亝倅亝倛丆侽亝倂亝倛乸
俠10亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆侽亝倄亝倛丆侽亝倅亝倛丆倛亙倂亝侾乸
俠11亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆侽亝倄亝倛丆倛亙倅亝侾丆侽亝倂亝倛乸
俠12亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆侽亝倄亝倛丆倛亙倅亝侾丆倛亙倂亝侾乸
俠13亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆倛亙倄亝侾丆侽亝倅亝倛丆侽亝倂亝倛乸
俠14亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆倛亙倄亝侾丆侽亝倅亝倛丆倛亙倂亝侾乸
俠15亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆倛亙倄亝侾丆倛亙倅亝侾丆侽亝倂亝倛乸
俠16亖乷乮倃丆倄丆倅丆倂乯乥倛亙倃亝侾丆倛亙倄亝侾丆倛亙倅亝侾丆倛亙倂亝侾乸
偨偩偟丄倛亖侾乛俀偱偡丅乮乽倛亝乿傪乽倛亙乿偵曄偊傞傢偗偱偡偹乯
丂
丂偙偆偡傞偲丄俠01偼嫍棧偑侾偺俀揰傪攝抲偱偒傑偡偑丄懠偺侾俆屄偺僽儘僢僋偼丄
攝抲偱偒傑偣傫丅
丂偟偨偑偭偰丄侾俈揰傪攝抲偡傞偨傔偵偼丄俠01偵俀揰丄懠偺侾俆僽儘僢僋偵偼侾揰
偢偮攝抲偡傞偙偲偵側傝傑偡丅
丂俠侽侾偺俀揰偺攝抲偼丄俉捠傝偁傞傢偗偱偡偑丄懳徧惈傪峫椂偡傞偲丄杮幙揑偵偼
俁捠傝偱偡丅
丂
嘆乮侽丆侽丆侽丆侽乯偲乮倛丆倛丆倛丆倛乯
丂乮倛丆倛丆倛丆倛乯偐傜偺嫍棧偑侾埲忋偺揰偼丄奺捀揰偟偐偁傝傑偣傫丅
丂偙偺働乕僗偱偼丄乽奺捀揰偵侾偮偢偮偲丄拞怱偵堦偮乿偺傒偲側傝傑偡丅
丂
嘇乮倛丆侽丆侽丆侽乯偲乮侽丆倛丆倛丆倛乯
丂偦傟偧傟偺揰偐傜丄乬椬偺僽儘僢僋乭偺揰偑妋掕偟傑偡丅
丂偙偆偟偰媮傑偭偨揰偵偮偄偰丄嵞搙乽乬椬偺僽儘僢僋乭偺揰乿傪媮傔傑偡丅
丂偟偐偟丄偨偲偊偽俠16偵偮偄偰偼丄僽儘僢僋慡懱偑丄乽媮傑偭偨揰乿偺侾偮偐傜侾
枹枮偺嫍棧偵偁傞偺偱丄揰傪攝抲偱偒傑偣傫丅
丂偟偨偑偭偰丄侾俈揰攝抲偡傞偙偲偼偱偒傑偣傫丅
丂
嘊乮倛丆倛丆侽丆侽乯偲乮侽丆侽丆倛丆倛乯
丂嘇偲摨條偵峫偊傑偡丅
丂傗偼傝俠16偑嫹偡偓傞偺偱丄侾俈揰攝抲偡傞偙偲偼偱偒傑偣傫丅
丂
丂偙偆偟偰丄乽係師尦挻棫曽懱偵偍偗傞丄憡屳偺嫍棧偑侾埲忋偺侾俈揰偺攝抲乿偼丄
侾捠傝偟偐偁傝偊側偄偙偲偑暘偐傝傑偡丅
丂
丂乽亀媮傑偭偨揰亁偺侾偮乿偼丄傗偼傝嬶懱揑偵偟偨傎偆偑傛偄偱偡偹丅
丂嘇偺応崌丄乮倛丆侽丆侽丆侽乯仺乮侾丆倛丆倛丆倛乯伕俠09
丂丂偁傞偄偼丄乮侽丆倛丆倛丆倛乯仺乮倛丆侾丆侾丆侾乯伕俠08
丂嘊偺応崌丄乮倛丆倛丆侽丆侽乯仺乮侾丆侾丆倛丆倛乯伕俠13
丂丂偁傞偄偼丄乮侽丆侽丆倛丆倛乯仺乮倛丆倛丆侾丆侾乯伕俠04
偱偡丅
丂
丂傕偭偲敪揥偝偣偰丄俆師尦挻棫曽懱偵俁俁揰傪攝抲偡傞栤戣傕峫偊偐偗傑偟偨偑丄
乽摨偠傛偆偵併俆乛俀乿偲偼偄偐側偄傜偟偄乮椺偺曐栘杮宐嶰巵傕俆師尦偺栤戣傪峫偊偐
偗偨巪儊乕儖偑偁傝傑偟偨丅乽旕悢妛揑婣擺朄偱併俆乛俀偩偑僟儊乿偩偦偆偱偡丅乯丅懡
暘侾偵側傞偲巚偄傑偡偑丅
丂偍偐偘偱丄偁偲侾侽侽擭偖傜偄偼丄偙傟偱梀傋偦偆偱偡丅
|
|
仭丂晲揷棽巌巵
堦曈偺挿偝侾偺挻棫曽懱撪偵侾俈屄偺揰傪丄
A0(0,0,0,0),A1(0,0,0,1),A2(0,0,1,0),A3(0,0,1,1),A4(0,1,0,0),A5(0,1,0,1),
A6(0,1,1,0),A7(0,1,1,1)A8(1,0,0,0),A9(1,0,0,1),A10(1,0,1,0),A11(1,0,1,1),
A12(1,1,0,0),A13(1,1,0,1),A14(1,1,1,0),A15(1,1,1,1),
A16(0.5,0.5,0.5,0.5)
偵攝抲偡傞偲丄嵟傕嬤偄2揰娫偺嫍棧偑嵟戝抣傪庢傞丅
偦偺嫍棧L偼丄
L=併(0.5^2+0.5^2+0.5^2+0.5^2)
L=1
夝摎丏侾
姶憐丗捈姶揑偵揰傪攝抲偟傑偟偨丅偙偺攝抲偑嵟慞偱偁傞帠偼丄攚棟朄偱擟堄偺揰傪
旝彫偵摦偐偟偰傒傟偽徹柧偱偒偦偆偱偡偹丅
偛巜揈偺曽朄偱偼丄嬊強揑偵偼嵟慞攝抲偲尵偊傞偐傕偟傟傑偣傫偑...
椺偊偽丄侾曈偺挿偝偑侾偺惓曽宍偵俇揰傪攝抲偡傞偙偲傪峫偊偰傒傑偟傚偆丅
丂
丂
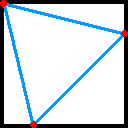
忋恾偺傛偆偵攝抲偡傞偲丄惵怓偺慄乮摍挿乯偱寢偽傟偨俀揰娫偺嫍棧偼乮併俈亅侾乯乛俁乮佮侽丏俆係俉丒丒丒乯偲側傝傑偡偑丄
偳偺侾揰傪旝彫偵摦偐偟偰傕嫍棧偑偙偺抣傛傝彫偝偔側傞俀揰偑偱偒偰偟傑偄傑偡丅
堦曽丄壓婰偺攝抲偱偼丄俀揰娫偺嫍棧偑俀亅併俀乮佮侽丏俆俉俆丒丒丒乯偲側傞偺偱丄忋恾偑嵟慞偺攝抲偱偼側偄偙偲偑傢偐傝傑偡丅
傕偭偲傕丄壓婰偺攝抲偑嵟慞偐偳偆偐傕傛偔傢偐偭偰偄傑偣傫偑丅
丂
偱丄栤戣偱偡丅
侾曈偺挿偝偑侾偺惓曽宍偵俈揰傪攝抲偟傑偡丅偙偺偲偒嵟傕嬤偄俀揰娫偺嫍棧偑側傞傋偔戝偒偔側傞傛偆偵偟偨偄偺偱偡偑丄偳偆偟偨傜偄偄偱偟傚偆偐丅
幚偼俉揰攝抲偺恾傛傝嫍棧傪戝偒偔偱偒偢擸傫偱偄傑偡丅
|

併俀 |
併俇亅併俀 |

侾 |
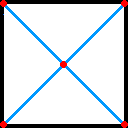
併俀乛俀 |
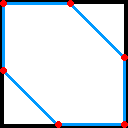
俀亅併俀 |
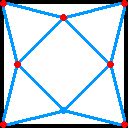
乮併俇亅併俀乯乛俀 |
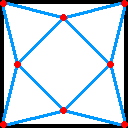
乮併俇亅併俀乯乛俀 |

侾乛俀 |
|
2005擭2寧4擔捛婰
丂
暯愇偝傫偐傜丄俇揰攝抲偺夵椙埬傪偄偨偩偒傑偟偨丅
丂
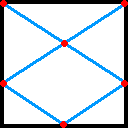 併侾俁乛俇
|
2005擭2寧11擔捛婰
丂
暯愇偝傫偐傜丄俈揰攝抲偺夵椙埬傪偄偨偩偒傑偟偨丅暯愇偝傫偺愢柧偲壓恾偺娭學偑傢偐傞傛偆偵丄俁揰攝抲埬傪廳偹偰彂偄偰偄傑偡丅
丂
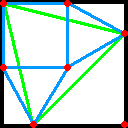 係亅俀併俁
丂乽惓曽宍偵俁揰乿偺寢壥傪棙梡偟傑偡丅
丂偁偺恾偱丄惓曽宍偺捀揰傪丄嵍忋偐傜斀帪寁夞傝偵丄俙丄俛丄俠丄俢偲偟傑偡丅
丂攝抲偝傟偨俁揰偺偆偪丄曈俛俠忋偺傕偺傪俹丄曈俠俢忋偺傕偺傪俻偲偟傑偡丅傕偆
侾揰偼俙偵堦抳偟傑偡丅
丂慄暘俙俹偺悅捈俀摍暘慄偲丄曈俙俛偺岎揰傪俼偲偟傑偡丅傑偨丄慄暘俙俻偺悅捈俀
摍暘慄偲曈俢俙偺岎揰傪俽偲偟傑偡丅
丂嵟屻偵丄慄暘俹俼偺悅捈俀摍暘慄偲丄懳妏慄俙俠偺岎揰傪俿偲偟傑偡丅
丂俙丄俹丄俻丄俼丄俽丄俿丄俠偺俈揰偼丄憡屳偺嫍棧偑丄偡傋偰丄乮併6亅併2乯乛2
傛傝戝偒偄偙偲偑帵偣傑偡丅
丂
丂偨偲偊偽俙俼偼丄俙俹偺拞揰傪偲傟偽乽捈妏嶰妏宍偺幬曈偼懠偺曈傛傝挿偄乿偲偄
偆掕棟偵傛傝丄俙俹乛2傛傝挿偄偙偲偑暘偐傝傑偡丅
丂俹俿傕丄俹俻偺拞揰傪偲傟偽丄摨條偵俹俻乛2傛傝挿偄偙偲偑暘偐傝傑偡丅仭
丂
丂偙偺攝抲偑嵟慞偺傕偺偐丄嬊抧揑偵傕丄傑偩暘偐傝傑偣傫丅偦傕偦傕乽嵟抁嫍棧乿
偺抣傕寁嶼偟偰偄傑偣傫乮寁嶼偟偐偗偨偺偱偡偑丄巹偺寁嶼擻椡偺晄懌傪妋擣偟偨偩
偗偱嵙愜偟傑偟偨乯丅
丂
丂乽惓嶰妏宍偵侾侽揰乿偲偄偆偺傕偁傝傑偟偨偹丅
丂惓嶰妏宍偵嶰妏悢乮亖値乮値亄侾乯乛2乯偼丄傒傫側僺儏僞僑儔僗偑峫偊偨攝抲偲
摨偠偵側傞傛偆側婥偑偟傑偡丅嶰妏悢埲奜偺丄偨偲偊偽俈揰偲偐偩偲丄偳偆側傞偐暘
偐傝傑偣傫丅
丂惓曽宍偵巐妏悢乮亖暯曽悢亖値**2乯偼丄値偑彫偝偄偲偒偼奿巕揰攝抲偵側傞傛偆
偱偡偑丄俆偖傜偄偐傜丄奿巕揰攝抲傛傝椙偄攝抲偑偁傝傑偡丅偙傟傕乽旕悢妛揑婣擺
朄乿偑巊偊側偄偱偡偹丅
丂墌偲偄偆偺傕偪傚偭偲峫偊傑偟偨丅俆揰傑偱偼廃忋偵攝抲偝傟傑偡丅俇揰偺応崌
偼丄廃忋偵俆揰丄拞怱偵侾揰偱傕壜偱偡丅俈揰偐傜偼丄拞怱偵侾揰偑昁恵偲側傝傑
偡丅傕偭偲懡偔偡傞偲丄撪晹偵俀揰丄俁揰偲憹偊偰偄偔偺偱偟傚偆偐丅
丂侾侽侽擭偳偙傠偐丄愮擭傕枩擭傕梀傋偦偆偱偡偹丅
|
2005擭2寧12擔捛婰
丂
忋恾偵曗彆慄傪壛偊傑偟偨丅偐偊偭偰傢偐傝偵偔偄丠
丂
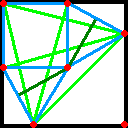 係亅俀併俁
|
|
仭丂愳暲梞懢巵
16屄偺捀揰偲拞怱(0.5,0.5,0.5,0.5)偵攝抲丅嶰暯曽偺掕棟傪3夞巊偆偲丄拞怱偲捀揰偺嫍棧偼1丅2偮偺捀揰偺嫍棧傕1丅傛偭偰摎偊偼1丅
丂
娙堈徹柧丅
捀揰偺揰傪摦偐偡偲拞怱偲嬤偔側傝丄拞怱偺揰傪摦偐偡偲偄偢傟偐偺捀揰偵嬤偔側傞丅
棫懱偵撪愙偡傞媴偺敿宎傪媮傔傠偲偄偭偨嫢埆側栤戣偵嬯偟傔傜傟偨偺傪巚偄弌偟傑偟偨丅
忋婰偺侾曈偺挿偝偑侾偺惓曽宍傊偺値乮亖俀乣俋乯揰攝抲埬偱偡偑丄
値亖俀丄俆偺応崌傪彍偄偰嵟慞偺徹柧偼峫偊偰偄傑偣傫丅
僄儗僈儞僩偵徹柧偱偒傑偡偐偹偉丅
|
|
仭丂暯愇巌巵
丂偼偠傔傑偟偰丅暯愇偲怽偟傑偡丅
丂偙偺僒僀僩偼丄曐栘杮偲偄偆彨婝婥偪乧偠傖側偐偭偨丄彨婝傪偙傛側偔垽偡桭恖偐
傜嫵傢傝傑偟偨丅
丂
丂懡暘丄惓夝偼侾偱偡丅
丂嬶懱揑側揰偺攝抲偼丄奺捀揰偵侾偮偢偮偲丄拞怱偵堦偮偱偡丅
丂侾偲偄偆抣偼丄曈傪嫴傓俀揰偺嫍棧偱偁傞偲摨帪偵丄拞怱偲奺捀揰偲偺嫍棧偱傕偁
傞偲偙傠偑堄奜偱柺敀偄偲巚偄傑偟偨丅
丂
丂乽懡暘乿偲偄偆偺偼丄柺敀偄偲巚偄偮偮傕丄妋怣偑柍偄偐傜偱偡丅
丂偙偺攝抲偐傜丄偳偺侾揰偁傞偄偼俀揰傪堏摦偝偣偰傕丄嵟抁偺嫍棧偼彫偝偔側偭偰
偟傑偄傑偡偑丄傕偭偲偨偔偝傫偺揰傪偆傑偔攝抲偟側偍偟偨傜丄傕偆彮偟挿偔偱偒傞
偺偱偼側偄偐偲峫偊偰偟傑偄傑偡丅偟偐偟崱偺偲偙傠丄偦偺傛偆側椺偼尒偮偗偰偄傑
偣傫丅
丂俀師尦傗俁師尦偱丄偁傞偄偼揰偺悢傪彮側偔偟偰丄摨條偺栤戣傪峫偊傞偲丄婔偮偐
偺働乕僗偱偼丄惓妋側攝抲偲嫍棧偑媮傑傝傑偟偨偑丄乽係師尦侾俈揰乿偲偄偆働乕僗
偺嶲峫偵偼側傝傑偣傫偱偟偨丅
曐栘杮偝傫偲偼丄亀戞21夞恄柍堦懓偺斆棓亁偵夝摎傪婑偣傜傟偰偄傞曐栘杮宐嶰偝傫偺偙偲偱偟傚偆偐丅
偲傕偁傟丄偛夝摎偁傝偑偲偆偛偞偄傑偡
丂
偙偺傛偆側栤戣偱偼旕忢偵尷傜傟傟偨働乕僗偱偟偐摎偑妋掕偱偒偰偄側偄傛偆偱偡丅
惉壥傪嫟桳偝偣偰傕傜偊傟偽偲巚偄傑偡丅
|
|