|
| 仭丂栤戣 |
丒 |
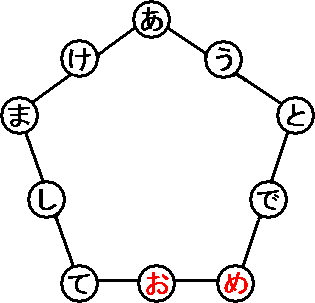
壓恾偺乬偁乭偐傜乬偆乭傑偱偺暥帤偵侽偐傜俋傑偱偺悢帤傪傂偲偮偢偮擖傟偰丄摨堦捈慄忋偁傞俁屄偺悢帤偺榓偑俆慻偲傕侾俇偵側傞傛偆偵偟偰偔偩偝偄丅 |
| 
|
|
丒 |
弰夞夝傗斀揮夝傪攔彍偡傞偨傔丄
偁亙傑丄偁亙偰丄偁亙傔丄偁亙偲丄傑亙偲
偲偟偰偍偒傑偡丅 |
|
| 仭丂夝摎 |
丒 |
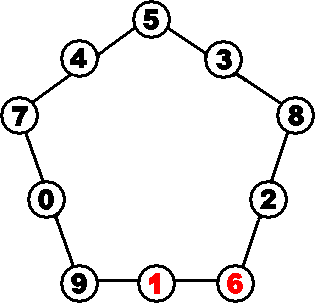
壓恾偺偲偍傝丅 |
| 
|
|
丒 |
夝摎幰偼壀揷廏堦巵丄恄柍幍榊巵丄杒懞懢楬巵丄恄柍敧媺巵丄戝栘彑桾巵丄庒椦峀巵丄偍傕偝傫巵乮杒懞巵偵傛傞戙棟夝摎乯丄愳暲梞懢巵丄偨偔傏傫巵偺俋柤乮夝摎摓拝弴乯丅慡堳惓夝偱偟偨丅 |
|
丒 |
尩惓側傞拪慖偺寢壥丄寽徿摉慖幰偼埲壓偺偲偍傝偲側傝傑偟偨丅
乽椻搥恖娫乿丗壀揷廏堦巵
|
|
| 仭丂夝愢 |
丒 |
乷偁丄偗丄傑丄...丄偆乸亖乷侽丄侾丄俀丄...丄俋乸側偺偱丄
偁亄偗亄傑亄...亄偆亖侽亄侾亄俀亄...亄俋亖係俆丒丒丒嘆
摨堦捈慄忋偺悢帤偺榓偼侾俇側偺偱丄
偁亄偗亄傑亖侾俇丒丒丒嘇
傑亄偟亄偰亖侾俇丒丒丒嘊
偰亄偍亄傔亖侾俇丒丒丒嘋
傔亄偱亄偲亖侾俇丒丒丒嘍
偲亄偆亄偁亖侾俇丒丒丒嘐
亪丂偁亄傑亄偰亄傔亄偲亖俁俆丂乮嘇亄嘊亄嘋亄嘍亄嘐亅嘆乯
亪丂乷偁丄傑丄偰丄傔丄偲乸亖乷俆丄俇丄俈丄俉丄俋乸
偙偺拞偱偼乬偁乭偑嵟彫側偺偱丄
偁亖俆丒丒丒嘑
傑亗俇丂乮佹丂傑亖俇丂仺丂偗亖侾俇亅偁亅傑亖俆亖偁両乯
偲亗俇丂乮佹丂偲亖俇丂仺丂傑亜偲両乯
亪丂偰亖俇丄傔亖俇丒丒丒嘒
傑亗俋丂乮佹丂傑亖俋丂仺丂傑亜偲両乯
亪丂偰亖俋丄傔亖俋丄偲亖俋丒丒丒嘓
嘑丄嘒丄嘓丄偍傛傃椬傝崌偭偨捀揰偑俉丄俋偲側傞乮偡偱偵榓偑侾俇傪挻偊偰偄傞乯偙偲偼側偄偙偲丄乬傑亙偲乭傪峫偊傞偲丄屲妏宍偺捀揰偺悢帤偵娭偟偰偼埲壓偺慻傒崌傢偣偟偐偁傝傑偣傫丅
乮偁丄傑丄偰丄傔丄偲乯亖
乮俆丄俉丄俇丄俈丄俋乯丄
乮俆丄俈丄俋丄俇丄俉乯丄
乮俆丄俈丄俉丄俇丄俋乯丄
乮俆丄俉丄俈丄俇丄俋乯
偙傟偐傜巆傝傪媮傔傞偲丄夝摎偺僷僞乕儞偺傒偑惗偒巆傞偙偲偑傢偐傝傑偡丅
|
|
仭丂壀揷廏堦巵
[偁偗傑偟偰偍傔偱偲偆]偺弴偵
5470916283
僾儘僌儔儉偱偙偆偄偭偨栤戣傪夝偔偺偑岲偒側偺偱夝偒傑偟偨丅
柺敀偐偭偨偱偡丅
偁傝偑偲偆偛偞偄傑偟偨丅
偙偙偺寽徿栤戣偼丄巻偲墧昅偱夝偗傞傪偙偲傪栚巜偟偰嶌偭偰偄傑偡丅偤傂巻偲墧昅偱傕僩儔僀偟偰傒偰偔偩偝偄丅
傕偭偲傕丄暿夝偑側偄偙偲偼擮偺偨傔僾儘僌儔儉傪慻傫偱妋偐傔偰傑偡偑丅
|
|
仭丂恄柍幍榊巵
恄柍幍榊偱偡
乮夝摎乯
丂偁偗傑偟偰偍傔偱偲偆
丂俆係俈侽俋侾俇俀俉俁
乮姶憐乯
丂0偐傜9傑偱偺崌寁偼45丅榓偑16亊5亖80偲偄偆偙偲偼丄廳暋偟偰
悢偊傜傟傞乽偁傑偰傔偲乿偼乽俋俉俈俇俆乿偺慻傒崌傢偣丅屻偼忦
審傪峫椂偟偰帋峴嶖岆偱夝偒傑偟偨丅乽偍傔乿亖乽侾俇乿偲偄偆偺
偼梊憐捠傝偱偟偨偑丄夝偔偲偒偼偙偺梊憐偼巊偭偰偄傑偣傫丅惓寧
偺懅敳偒偵庤崰側椙偄栤戣偩偲巚偄傑偡丅
乽偍傔乿亖乽侾俇乿偼丄慱偭偰偄傟偨傕偺偱偼側偔偰丄偨傑偨傑婥偯偄偨傕偺丅栤戣偑偪傚偭偲堈偟夁偓偨傛偆側偺偱丄懡彮偼僾儔僗億僀儞僩偵側傞偐偲巚偄庯岦偺傆傝傪偟偰傒傑偟偨丅
|
|
仭丂杒懞懢楬巵
杒懞偱偡丅
寽徿侾俇偺栤戣偱妝偟傑偣偰捀偄偨偺偱帺暘偺峫偊偨夝朄傪憲傜偝偣偰偄偨偩偒傑偡丅
壛嶼婰崋傪婰弎偡傞偲尒偨栚偑偛偪傖偛偪傖偡傞偺偱埲壓偺婰朄傪庢傝擖傟傑偡丅
婰朄丗乽俙俛乿偲彂偄偨傜丄俙亄俛偲偄偆堄枴偲偟傑偡丅
乽俙俛俠乿偲彂偄偨傜丄俙亄俛亄俠偲偄偆堄枴偱偡丅
乽俙俛乿亖俙亄俛丄乽俙俛俠乿亖俙亄俛亄俠
栤戣傛傝
乽偁偗傑乿亖侾俇丄乽傑偟偰乿亖侾俇丄乽偰偍傔乿亖侾俇丄乽傔偱偲乿亖侾俇丄乽偲偆偁乿亖侾俇
忋婰俆幃偺嵍曈偲塃曈偲傪偦傟偧傟懌偟崌傢偣傞偲丄
乽偁偗傑傑偟偰偰偍傔傔偱偲偲偆偁乿亖俉侽丂丒丒丒幃侾
傑偨丄偁偗傑偟偰偍傔偱偲偆丄偺奺暥帤偼偦傟偧傟侽乣俋偵懳墳偡傞偺偱
乽偁偗傑偟偰偍傔偱偲偆乿亖係俆丂丒丒丒幃俀
幃侾偺椉曈偐傜幃俀傪堷偔偲
乽傑偰傔偲偁乿亖俉侽亅係俆亖俁俆
傑偨
乽偗偟偍偱偆乿亖乽偁偗傑偟偰偍傔偱偲偆乿亅乽傑偰傔偲偁乿亖係俆亅俁俆亖侾侽
偝偰丄偗偟偍偱偆丄偺奺暥帤偼侽乣俋偺憡斀偡傞悢帤偵奩摉偡傞偺偱丄俆偮偺悢帤偺
慻傒崌傢偣偼侽丆侾丆俀丆俁丆係偺応崌偟偐偁傝偊傑偣傫丅
傑偰傔偲偁丄偺俆暥帤傕俆丆俇丆俈丆俉丆俋偺慻傒崌傢偣偱側偄偲崌寁偟偰俁俆偵側傝傑偣傫丅
偮傑傝丄奺捀揰偺悢帤偼俆丆俇丆俈丆俉丆俋丅奺曈偺悢帤偼侽丆侾丆俀丆俁丆係偵側傝傑偡丅
師偵曈偺悢抣偑侽偺偲偒偵丄椉捀揰偺悢帤偑偄偔偮偵側傞偐丄偲偄偆偙偲偱偡偑丄俀捀揰偺悢帤傪
懌偟偰侾俇偵側傞慻傒崌傢偣偼俈丆俋偺慻偟偐偁傝偊側偄偺偱丄偙偺慻偵寛傑傝傑偡丅
偱偼丄俋偺侽偱偼側偄曽偺傕偆堦曈偺偦傟偧傟曈丄捀揰偺悢帤偼偄偔偮偵側傞偐丠偲偄偆偲丄
傕偟丄捀揰偺悢帤傪俉偲壖掕偡傞偲偦偺帪揰偱椉捀揰偺悢帤偺崌寁偑侾俇傪墇偊傞偺偱丄
俉偑椬偺捀揰偵偔傞壜擻惈偼偁傝傑偣傫丅
師偵椬偺捀揰傪俆偲壖掕偟傑偡丅偦偆偡傞偲丄俋偺懳柺偵偁偨傞曈偺椉捀揰偼巆偭偨俇偲俉偲偄偆
偙偲偵側傝傑偡偑丄俆丆俋偺捀揰娫偺曈偺悢抣傕侾俇亅俋亅俆亖俀偲側傝丄傑偨俇丆俉偺捀揰娫偺
曈偺悢抣傕侾俇亅俇亅俉亖俀偲側傞偺偱丄慡偰偺暥帤偑堘偆悢帤偵側傞丄偲偄偆栤戣偺忦審偵堘斀
偡傞偙偲偵側傞偺偱丄椬偺捀揰偑俆偱偁傞丄偲偄偆壖掕偑娫堘偭偰偄偨偙偲偵側傝傑偡丅
傛偭偰俋偺椬偺捀揰偼丄俈偲俇偱偁傞丅偲偄偆偙偲偵側傝傑偡丅
懕偄偰俇偺傕偆堦偮偺椬偺捀揰偼丄俆偲俉偺偳偪傜偑擖傞偐丠偲偄偆栤戣偱偡偑丄傕偟俆傪擖傟傞偲
俇偲俆偺捀揰偺娫偺曈偵擖傞抣偑侾俇亅俇亅俆亖俆偲偄偆偙偲偵側傝丄奺暥帤偵懳墳偡傞悢帤偑憡斀
偡傞偲偄偆忦審傪枮偨偝側偄偺偱丄俇偺椬偺捀揰偼俉偲偄偆偙偲偵側傝傑偡丅
傛偭偰丄奺捀揰偺椬摨巑偺娭學偑俈丒俋丒俇丒俉丒俆丒俈偲偄偆娭學偱娐傪偮偔傞偙偲偑傢偐傝傑偡丅
奺捀揰偺暥帤偲悢帤偺懳墳偱偡偑丄偁亙傑丄偁亙偰丄偁亙傔丄偁亙偲丄傑亙偲偺娭學偐傜嵟彮偺悢帤
偼丄偁丄偺暥帤偵懳墳偡傞偺偱丄偁亖俆丄椬偺捀揰偵懳墳偡傞丄傑丄偲丄偺俀暥帤偼俈偲俉偵懳墳偟
傑偡偑丄傑亙偲丄偺娭學偐傜丄傑亖俈丄偲亖俉丅偝傜偵娐偺弴斣偐傜丄偰亖俋丄傔亖俇丄偲寛傑傝傑偡丅
栤戣偵栠偭偰丄奺暥帤偵悢帤傪摉偰偼傔傞偲
乽俆偗俈乿亖侾俇丄乽俈偟俋乿亖侾俇丄乽俋偍俇乿亖侾俇丄乽俇偱俉乿亖侾俇丄乽俉偆俆乿亖侾俇
傛偭偰丄偗亖係丄偟亖侽丄偍亖侾丄偱亖俀丄偆亖俁丄偲側傝傑偡丅
摎丗偁亖俆丄偗亖係丄傑亖俈丄偟亖侽丄偰亖俋丄
丂丂偍亖侾丄傔亖俇丄偱亖俀丄偲亖俉丄偆亖俁
丂丂丂丂丂俆
丂丂丂係丂丂丂俁
丂俈丂丂丂丂丂丂丂俉
丂丂侽丂丂丂丂丂俀
丂丂丂俋丂侾丂俇
嵟弶偼帋峴嶖岆偱杽傔偰偄偙偆偐偲巚偭偰偄偨偺偱偡偑丄傎偲傫偳棟孅偩偗偱丄慡偰
杽傔傞偙偲偑偱偒偰
嬃偒傑偟偨丅棟孅傪愢柧偡傞偺偑壓庤偱挿暥偵側偭偰偟傑偄丄偡偄傑偣傫丅
偍傔丄偺晹暘偑愒帤偵側偭偰偄偨偺偱丄偒偭偲侾偲俇偵側傞傫偩側偲巚偭偰偄傑偟偨
偑丄偦偺捠傝偵
側傞偲偙傠偑傑偨丄偟傖傟偰偄傞側丄偲巚偄傑偟偨丅
椡嶌夝摎偁傝偑偲偆偛偞偄傑偡丅
偲偙傠偱丄儂乕儉儁乕僕偱偙偺寽徿栤戣傪愰揱偟偰偄偨偩偒偁傝偑偲偆偛偞偄傑偟偨丅
亀巹偺掜巕乣亁傕妝偟偄偱偡偑丄屄恖揑偵偼亀乣憳擄擔婰亁偺暅妶傪婜懸偟偰偍傝傑偡丅
|
|
仭丂恄柍敧媺巵
壣偮傇偟偵峫偊偰傒偨丅
丂偁亖俆丄偗亖係丄傑亖俈丄偟亖侽丄偰亖俋丄
丂偍亖侾丄傔亖俇丄偱亖俀丄偲亖俉丄偆亖俁
偱崌偭偲傞偐丠
敿暘枹枮寁嶼丄敿暘埲忋摉偰偼傔
崌偭偲傞丅
壣偮傇偟偵側偭偰丄傛偐偭偨偭傌丅
戞俀怣
慜夞夝摎傪憲偭偨嵺偼丄彂偔偺偑柺搢偩偭偨偺偱乽敿暘枹枮寁嶼丄敿暘埲忋摉偰偼傔乿偲偟偐僐儊儞僩偟側偐偭偨偑丄偄偪偍偆偦偺拞恎傪柧傜偐偵偟偰偍偙偆偲巚偆丅
丂丂丂偁亄偗亄傑亖侾俇丒丒丒乮侾乯
丂丂丂傑亄偟亄偰亖侾俇丒丒丒乮俀乯
丂丂丂偰亄偍亄傔亖侾俇丒丒丒乮俁乯
丂丂丂傔亄偱亄偲亖侾俇丒丒丒乮係乯
丂丂丂偲亄偆亄偁亖侾俇丒丒丒乮俆乯
丂偺曈乆傪壛偊傞偲丄
丂丂丂乮偁亄傑亄偰亄傔亄偲乯亊俀亄偗亄偟亄偍亄偱亄偆亖俉侽
丂偲側傞丅偲偙傠偑丄偁乣偆偺憤榓亖侽乣俋偺憤榓亖係俆偱偁傞偐傜丄
丂丂丂偁亄傑亄偰亄傔亄偲亖俁俆丒丒丒乮A乯
丂偱偁傝丄偟偨偑偭偰丄偗亄偟亄偍亄偱亄偆亖侾侽丒丒丒乮B乯
丂偱偁傞丅
丂丂乮A)傛傝丄偁丄傑丄偰丄傔丄偲亖俆乣俋偺偄偢傟偐丄
丂丂乮B乯傛傝丄偗丄偟丄偍丄偱丄偆亖侽乣係偺偄偢傟偐
丂偑暘偐傞丅
丂丂偲偙傠偑丄偁亙傑丄偰丄傔丄偲偱偁傞偐傜丄偁亖俆偲寛傑傞丅
丂偁偲偼丄乮侾乯乣乮俆乯偵摉偰偼傔側偑傜丄弴師寛傔偰偄偭偨丅
埲忋偑丄巚峫夁掱偩丅
寢峔巚峫偟偲傞側丅
|
|
仭丂戝栘彑桾巵
偁丗俆
偗丗係
傑丗俈
偟丗侽
偰丗俋
偍丗侾
傔丗俇
偱丗俀
偲丗俉
偆丗俁
戞俀怣
丂丂丂丂俙
丂丂傾丂丂丂僆
俛丂丂丂丂丂丂丂俤
丂僀丂丂丂丂丂僄
丂丂俠丂僂丂俢
忋恾偺傛偆偵婰崋傪妱傝摉偰傞丅
侽乣俋側偺偱丄慡晹偺崌寁偼
乮俙亄俛亄俠亄俢亄俤乯亄乮傾亄僀亄僂亄僄亄僆乯亖係俆
奺曈偺寁偼偦傟偧傟侾俇側偺偱丄
侾俇仏俆亖俀仏乮俙亄俛亄俠亄俢亄俤乯亄乮傾亄僀亄僂亄僄亄僆乯亖俉侽
亪丂俙亄俛亄俠亄俢亄俤亖俉侽亅係俆亖俁俆
亪乮俙丆俛丆俠丆俢丆俤乯亖乮俆丆俇丆俈丆俉丆俋乯@弴晄摨
丂乮傾丆僀丆僂丆僄丆僆乯亖乮侽丆侾丆俀丆俁丆係乯@弴晄摨
壖偵僂亖侽偲偡傞偲丄俠丄俢偼俈偲俋丅
壖偵俠亖俈丄俢亖俋丂偲偡傞丅
乮夞揮傗斀揮偼嵟屻偵廋惓丅乯
俆偲俇偼椬傝崌偆捀揰偵偼側傜側偄偺偱丄俙亖俉
俙丒傾丒俛丂偲丂俙丒僆丒俤丂偼丄俉丒俁丒俆丂偲丂俉丒俀丒俇丅乮偳偭偪偑偳偭偪偐偼枹掕丅乯
丒丒丒偙偙傑偱偔傞偲捈姶偱悢帤傪偁偰偼傔偨曽偑憗偄偗偳丄傓傝傗傝棟媗傔偱嵟屻傑偱峴偔偲丄
乮俛丆俤乯亖乮俆丆俇乯@弴晄摨
乮僀丆僄乯亖乮侾丆係乯@弴晄摨丂丂佹侽丆俀丆俁偱偼側偄偺偱丅
俠亖俈丄俢亖俋丂偼偄偢傟傕婏悢側偺偱丄俛亄僀丄俤亄僄丂偼偄偢傟傕婏悢丅佹侾俇偼嬼悢側偺偱丅
亪俆偲係丄俇偲侾丂偑偦傟偧傟儁傾偲側傞丅
懌偟偰侾俇偵側傞偨傔偵偼丄俆丒係丒俈丂偲丂俇丒侾丒俋丂偲偄偆慻傒崌傢偣偵側傞丅
亪俛亖俆丄俤亖俇丄僀亖係丄僄亖侾
丂丂丂丂俉
丂丂俁丂丂丂俀
俆丂丂丂丂丂丂丂俇
丂係丂丂丂丂丂侾
丂丂俈丂侽丂俋
偲側傞偑丄忦審傛傝丄塃夞傝偵侾乛俆夞揮偝偣傞丅斀揮偼晄梫丅
丂丂丂丂俆
丂丂係丂丂丂俁
俈丂丂丂丂丂丂丂俉
丂侽丂丂丂丂丂俀
丂丂俋丂侾丂俇
俙.丂偁亖俆丄偗亖係丄傑亖俈丄偟亖侽丄偰亖俋丄偍亖侾丄傔亖俇丄偱亖俀丄偲亖俉丄偆亖俁
傢偞傢偞夝朄傪憲偭偰偄偨偩偒偁傝偑偲偆偛偞偄傑偟偨丅
奆偝傫旝柇偵夝朄偵堘偄偑偁傞偺偑妝偟偄偱偡偹丅
|
|
仭丂庒椦峀巵
庒椦偱偡丅擭夑寽徿丄偺偙偺偙偲夞摎偟傑偡丅
<夞摎>
偁5
偗4
傑7
偟0
偰9
偍1
傔6
偱2
偲8
偆3
<夝朄>
侐慜採
丒恾忋偵懚嵼偡傞5捠傝偺榓偵偼丄0乣9偺偆偪5庬椶偺悢帤偑1夞偩偗丄
偦偺懠偺5庬椶偺悢帤偑2夞偢偮偁傜傢傟傞丅
丒5捠傝偺榓傪嶌傞悢帤偺慻偼丄1夞偩偗尰傟傞悢帤傂偲偮偲丄
2夞尰傟傞悢帤2偮偱峔惉偝傟傞丅
丒0乣9偺堎側傞俁悢偱榓偑16偵側傞偺偼傢偢偐9捠傝丅
昞偵偟偰偍偔偲妝丅
侐揥奐
0傪娷傓偺偼"0,7,9"偺傒側偺偱嵦梡丅
7,9偼傕偆堦搙搊応偡傞丅
偲偄偆偙偲偼丄巆傝偼忋婰埲奜偱7傪娷傓慻傒崌傢偣傂偲偮偲丄
9傪娷傓慻傒崌傢偣傂偲偮丄偦偟偰7,9傪娷傑側偄慻傒崌傢偣2偮偱偁傞丅
7,9傪娷傑側偄慻傒崌傢偣偼"2,6,8","3,5,8"偟偐側偄偺偱嵦梡丅
偙偙偱1偵栚傪岦偗傞丅1傪娷傓慻傒崌傢偣偼"1,7,8"偲"1,6,9"偑偁傞偑丄
"1,7,8"偼"8"偑3夞栚偺搊応偲側傞偺偱媝壓丅"1,6,9"傪嵦梡丅
堦搙傕搊応偟偰偄側偄4,2夞栚偺搊応傪偟偰偄側偄7傪娷傓"4,5,7"傪嵦梡丅
偙傟偱慖戰偑廔椆丅
偁偲偼搊応夞悢傪峫椂偡傟偽婡夿揑偵娐偑偮偔傟傞丅
巜掕忦審偵崌傢偣偰夞揮/嬀憸傪嶌傞丅
<姶憐>
夁嫀偺栤戣偵斾傋傞偲僔儞僾儖丅
偍庤寉偱偼偁傞偗傟偳丄傕偆偪傚偭偲側偵偐偁傞偲婐偟偄偐傕丅
亀0乣9偺堎側傞俁悢偱榓偑16偵側傞偺偼傢偢偐9捠傝亁傪昞偵偟偰傒傑偟偨丅
| 0 | 7 | 9 |
| 1 | 6 | 9 |
| 1 | 7 | 8 |
| 2 | 5 | 9 |
| 2 | 6 | 8 |
| 3 | 4 | 9 |
| 3 | 5 | 8 |
| 3 | 6 | 7 |
| 4 | 5 | 7 |
側傞傎偳丄偙偺昞傪愭偵嶌偭偰偍偗偽妝偵夝偗傑偡偹丅姶暈偱偡丅
嬼悢偼側偤偐栤戣壔偑擄偟偄偱偡丅棃擭偼婏悢擭側偺偱婃挘傝傑偡丅
|
|
仭丂偍傕偝傫巵
侾俇傪嶌傞偺偵侽偑擖傞偺偼俈丄俋丄侽偺侾捠傝側偺偱侽偼妏偵偼偙側偄丅
俋亅侽亅俈偲偄偆曈偑偁傞偙偲偵側傞丅
巆傝偺曈偼俋亅俙亅俛丄俛亅俠亅俢丄俢亅俤亅俥丄俥亅俫亅俈偲側傞偺偩偑丄係曈偺崌寁偼俇係偩偐傜
俙亄俀俛亄俠亄俀俢亄俤亄俀俥亄俫亖係俉
俙亄俛亄俠亄俢亄俤亄俥亄俫亖俀俋側偺偱
俛亄俢亄俥亖侾俋
偮傑傝丄俛丄俢丄俥偼俆丄俇丄俉偺偄偢傟偐偲側傞丅
俆偲俇偼偲側傝偁偆妏偵偼擖傜側偄偺偱俢偺俉偑妋掕偡傞丅
乮側傫偰偺偼偁偲偱峫偊偨偙偲丅捈姶偱俢偑俉偐側偲巚偭偰傗偭偨傜偱偒偪傖偭偨乯
俢偑俉偵側傞偲俠丄俤偼俀丄俁偺偄偢傟偐偵側傞丅
偺偙傝偼侾偲係側偺偱丄
俙偑侾丄俛偑俇丄俠偑俀丄俢偑俉丄俤偑俁丄俥偑俆丄俫偑係偑妋掕偡傞丅
偁亙傑丄偁亙偰丄偁亙傔丄偁亙偲丄傑亙偲
側偺偱
偁亖俆
偗亖係
傑亖俈
偟亖侽
偰亖俋
偍亖侾
傔亖俇
偱亖俀
偲亖俉
偆亖俁
偵側傝傑偡丅
杒懞偝傫丄偍傕偝傫偺夝朄揮憲偁傝偑偲偆偛偞偄傑偟偨丅
乮堦晹昞婰儈僗偲巚傢傟傞偲偙傠偼廋惓偟傑偟偨乯
傑偨忋婰偩偗偱偼偪傚偭偲暘偐傝偯傜偄偲巚偆偺偱丄俈丄俋丄侽偑攝抲妋掕偟偨帪揰偺偱婰崋攝抲傪彂偄偰傒傑偟偨丅
丂丂丂丂俥
丂丂俫丂丂丂俤
俈丂丂丂丂丂丂丂俢
丂侽丂丂丂丂丂俠
丂丂俋丂俙丂俛
仈俧偼偳偙偵峴偭偨偺偩傠偆丠
|
|
仭丂愳暲梞懢巵
偁俆丂偗係丂傑俈丂偟侽丂偰俋丂偍侾丂傔俇丂偱俀丂偲俉丂偆俁
侾俇倶俆亖俉侽
俉侽亅侽亅侾亅俀亅俁亅係亅俆亅俇亅俈亅俉亅俋亖俁俆
侽亄侾亄俀亄俁亄係亄俆亄俇亄俈亄俉亄俋亅俁俆亖侾侽
侾侽亖侽亄侾亄俀亄俁亄係
傛偭偰曈偵侽乣係丂捀揰偵俆乣俋
偁偼捀揰偱嵟彫側偺偱俆
傑丂傗丂偲丂偵俇偑偔傞偲偗丂傗丂偆丂偵俆偑棃傞偺偱幐攕丂丂偰丂偐丂傔丂偵俇
傑亄偰丂偲丂傔亄偲丂偑堘傢側偗傟偽丂偟丂偲丂偱丂偑摨偠偵側傝幐攕
俆亄傑丂傑偨偼丂俆亄偲丂亖丂偰亄傔乮俇亄仈乯丂偩偲丂偗亖偍偱幐攕
仈偑俈丄俉偩偲丂忋偺幃偑惉棫偡傞偺偱丂幐攕
仈偼偺偙傝偺俋
俋亄俉亖侾俈亜侾俇側偺偱俋丆俉偼傔丄傑丂傑偨偼丂偰丄偲
傑亙偲丂傛傝丂傑亖俈丂偲亖俉丂偙傟偲忋傛傝丂偰亖俋丂傛偭偰丂傔亖俇
偙偺僞僀僾偺僷僘儖偑偡偒偱愄偵杺曽恮傪嶌偭偨傝偟偰偄傑偟偨
幚偼偙偺栤戣偺尦僱僞傕杺曽恮側偺偱偡丅
乮撌乯屲妏宍傪彂偄偰丄偝傜偵懳妏慄傪偡傋偰堷偒傑偡丅偡傞偲屲妏宍偑侾侾屄偺晹暘偵暘妱偝傟傑偡丅
偦偙偵侾乣侾侾偺悢帤傪摉偰偼傔丄屲妏宍偺捀揰傪捀揰偲偡傞嶰妏宍乮侾侽捠傝偁傝傑偡乯偺撪晹偺悢帤偺榓偑
堦掕偵側傞傛偆偵偡傞杺曽恮偱偡丅
偆傑偔傾儗儞僕偱偒偨偲巚偭偰偄傑偡丅
|
|
仭丂偨偔傏傫巵
KAMINA PUBLICATIONS丂寽徿侾俇夝摎
偁丒丒俆
偗丒丒係
傑丒丒俈
偟丒丒侽
偰丒丒俋
偍丒丒侾
傔丒丒俇
偱丒丒俀
偲丒丒俉
偆丒丒俁
幍榊偝傫偺宖帵斅傪尒偰傗偭偰偒傑偟偨丅榑棟揑夝朄傕偁傞偺偱偟傚偆偑丄寢嬊庤嶌嬈偱夝偄偰偟傑偄傑偟偨丅
庤嶌嬈偱夝偗偰偟傑偆偺偑僀儅僀僠偱偡偐偹丅
棃擭偼榬椡偱偼偳偆偵傕側傜側偄傕偺偵偟傛偆偐側偀丅乮慺嵽偼偁傞乯
|
|

